时间复杂度

算法的时间复杂度是T(n), T是time，它与问题规模n的大小有关，且可以事先预估时间。因为时间复杂度的函数在n规模大时，其颇为复杂，**因此在问题规模足够大时，可以忽略表达式中的低阶部分，**即只保留时间开销表达式最高阶的那部分，如T(n)=n的三次方+n的二次方+99999，只需要保留n的三次方即可。经典的抓大放小

甚至可以去掉系数，如3n简化为n，因为3000和9000依然是一个数量级的，但是n和n的平方相差的数量级就极大。

结论：

• 顺序执行的代码只会影响常数列，可以忽略；
• 只需要挑循环中的一个基本操作，分析它的执行次数与n的关系即可。如循环3000次而代码执行了3000次则为n，执行9000次为3n，再省略常数项依然是n；
• 如果有多层嵌套循环，只需关注最深层循环循环了几次 ;如循环3000次而代码执行了 3000的平方 的话，则时间复杂度函数是O(n的平方)

即函数是 循环次数与最深层代码循环的关系，如3000对9000则是3n; 3000对9000000则是n的平方

算法的性能问题只有在n很大的时候才会暴露出来

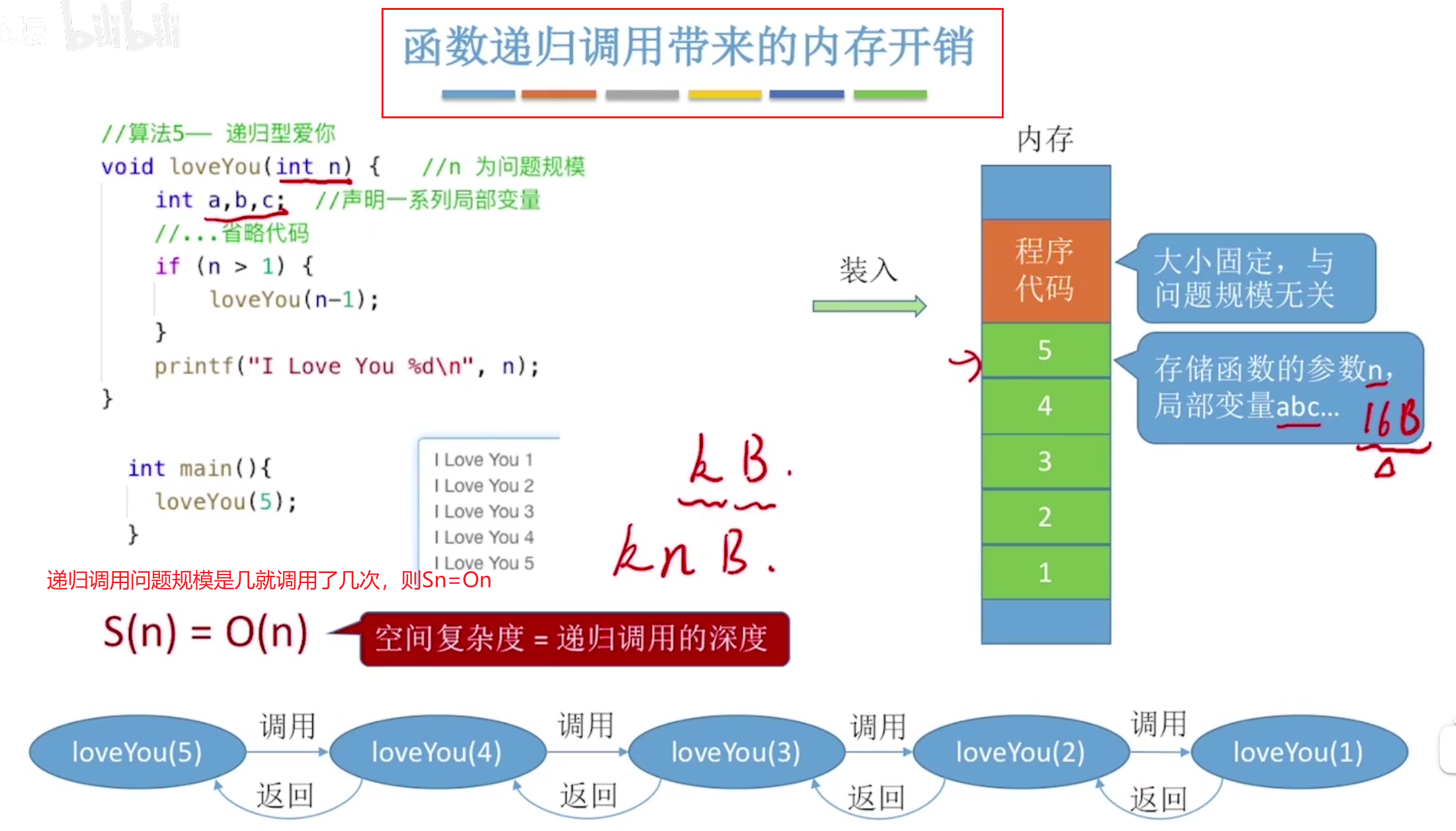
空间复杂度

和时间复杂度一样，都是分析所占空间大小和问题规模的关系

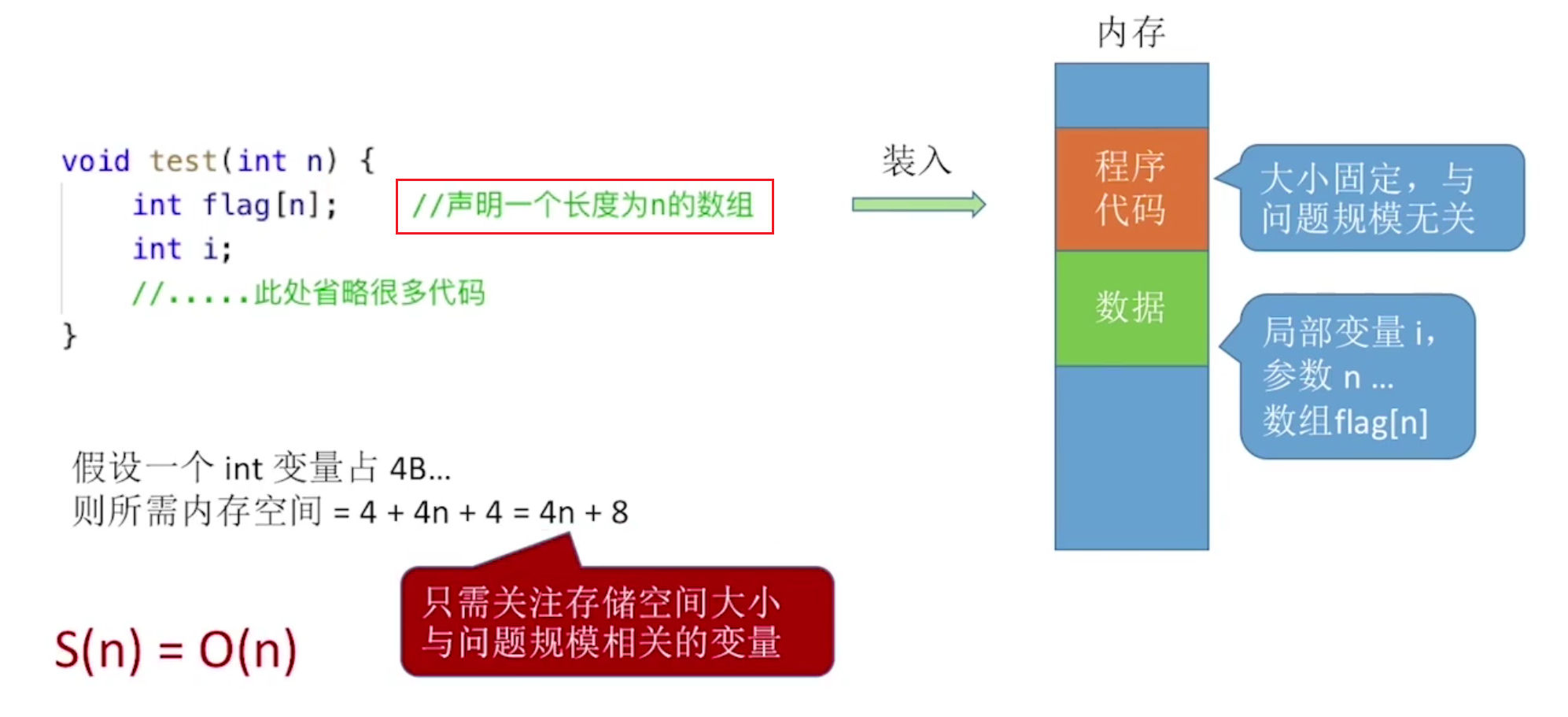
和时间复杂度类似，只需要关注和问题规模相关的变量即可。即当n变为无穷时，对应的变量的内存消耗是否会跟着改变

数据的逻辑结构

集合

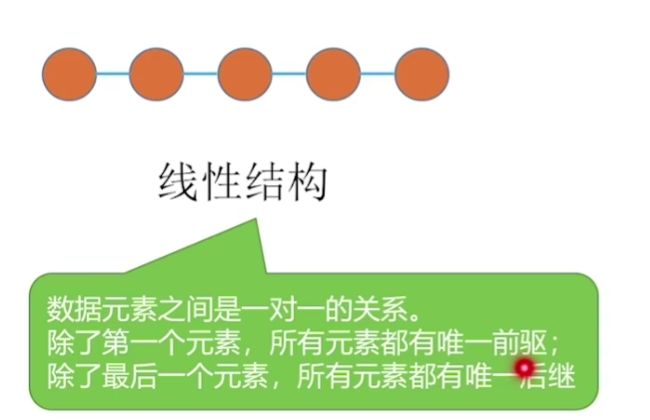
线性结构

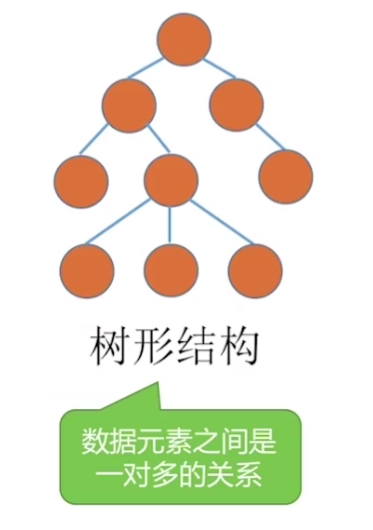
树形结构

图状结构

数据的存储结构

顺序存储

链式存储

每个元素在存储自己的数据元素的同时还会额外存储下一个元素的指针，以便指向下一个元素

单链表

带头节点的头节点不存储数据，但是会存储下一个节点的指针。仅仅是之后实现基本操作时更方便些，可以实现如果要在最开头插入一个节点，修改头节点的next和新增节点的next即可

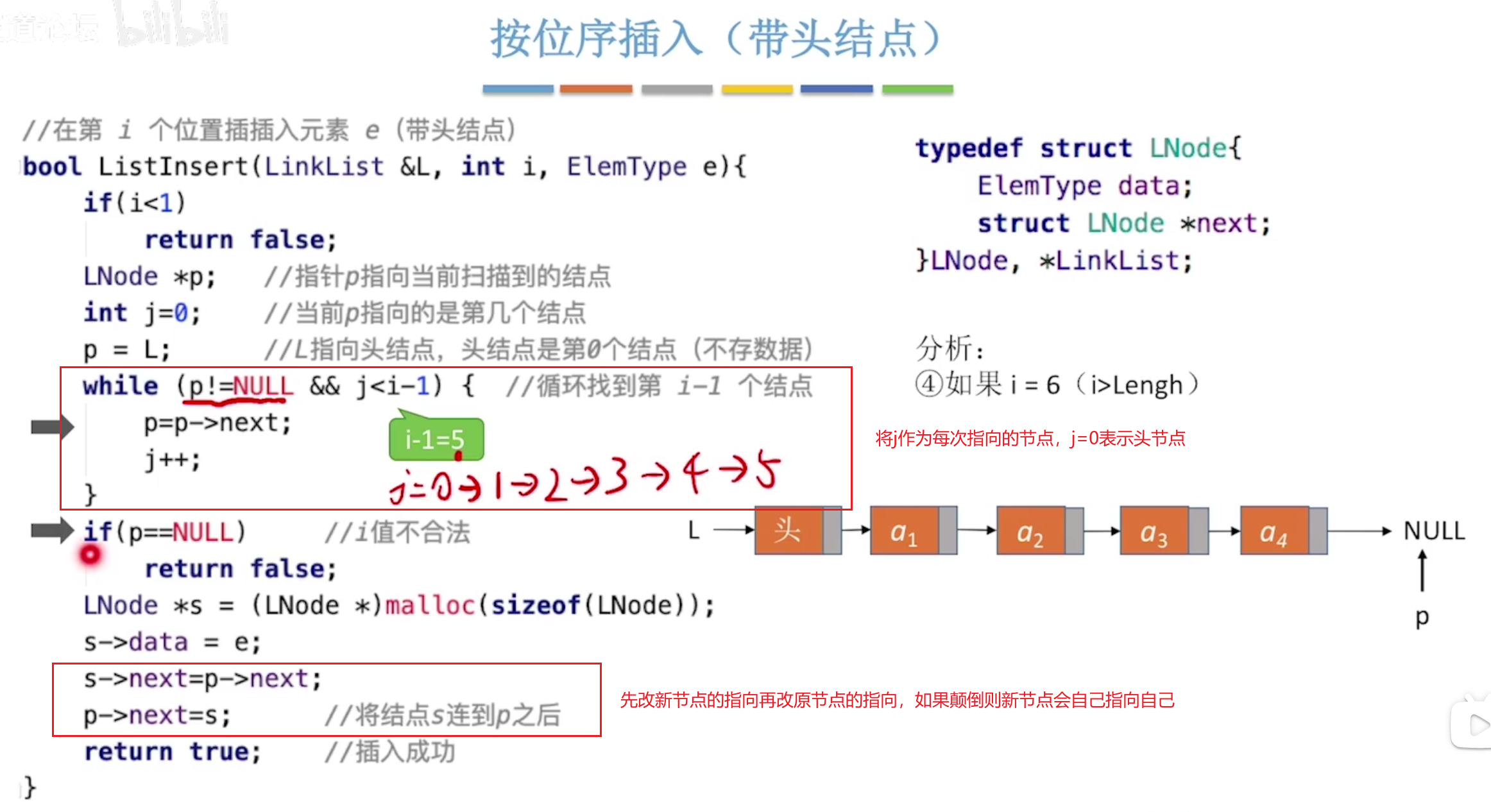
下面是带头节点的情况，这种是最常使用的。头节点设为第0个。如果不带头节点则最开始的判断可以让其在0时进行赋值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

type LNode struct {
	data string
	next *LNode
}

func main() {
	L := new(LNode)
	// 在某个节点后插
	insertList(L, 1, "abc")
	insertList(L, 2, "def")
	// 在某个节点前插(两个next则是在2节点之前，从0头节点开始计数)
	insertListTwo(L.next.next, "obg")
	// 删除某个节点
	deleteList(L, 3)
	for {
		// 先运行一次L=L.next是去除头指针，头指针是没有数据的
		L = L.next
		if L == nil {
			return
		}
		fmt.Println(L.data)
	}
}

func insertList(LinkList *LNode, i int, data string) {
	if i < 0 {
		return
	}
	var p *LNode
	p = LinkList
	j := 0 // j表示当前所在节点，最开始是0即头节点，通过if向下循环到需要操作的节点
	// 当i为1表示在1节点插入数据，不会走此循环，即将头节点的next给了p 1节点,头节点换存p节点的指针
	for k := 0; k < i; k++ {
		if p != nil && j < i-1 {
			p = p.next
			j++
		}
	}
	S := new(LNode)
	S.data = data
	S.next = p.next
	p.next = S
	return
}

func insertListTwo(LinkList *LNode, data string) {
	if LinkList == nil {
		return
	}
	S := new(LNode)
	S.data = data
	S.data, LinkList.data = LinkList.data, S.data
	S.next = LinkList.next
	LinkList.next = S
}

func deleteList(LinkList *LNode, i int) {
	if i < 0 {
		return
	}
	var p *LNode
	p = LinkList
	j := 0
	for k := 0; k < i; k++ {
		if p != nil && j < i-1 {
			p = p.next
			j++
		}
	}
	if p == nil {
		return
	}
	if p.next == nil { // 第i-1个节点已经是nil了，则无法删除第i个节点
		return
	}
	q := p.next     // 删除节点则是i-1的q节点的下一个 next
	p.next = q.next // 将删除节点的下一个节点赋值给p,则为上一个节点
	// 释放q
	q = nil
	return
}

尾插法建立单链表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

	var x string
	L := new(LNode)
	r := L
	fmt.Scanln(&x)
	for {
		if x != "9999" {
			s := new(LNode)
			s.data = x
			r.next = s
			// 让r的指针永远指向最后一个元素。
			r = s
			fmt.Scanln(&x)
		} else {
			// 这里将r.next变为nil是避免野指针的情况发生，即不为空有可能会指向内存中未知的指针中的数据[在C中会发生，但在go中用new初始化时会将结构体中的数据都进行零值初始化。但是加上是一个好习惯]
			r.next = nil
			break
		}
	}
	for {
		fmt.Println(L, L.next)
		if L.next == nil {
			return
		}
		L = L.next
	}

单链表的逆置

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

	p := T.next
	// 在此处将T进行断链，非常重要的一步。
	T.next = nil
	for {
		if p == nil {
			break
		}
		// 存储p的下一个节点
		k := p.next
		// T.next最开始是nil，即指向虚无，第二次循环时T的next已经是原来的p1了，即p2.next=p1,再将T头指针的next指向p,现在就是头-p2-p1
		// 再次循环，此时k存储的是p3,p是p2，将p2的next存储为T.next即p2-p1
		// 下面两句就是非常常规的头插法代码
		p.next = T.next
		T.next = p
		p = k
	}

双链表就是每个节点存了前一个和后一个的指针、循环单/双链表则是最后一个节点又指向了头指针

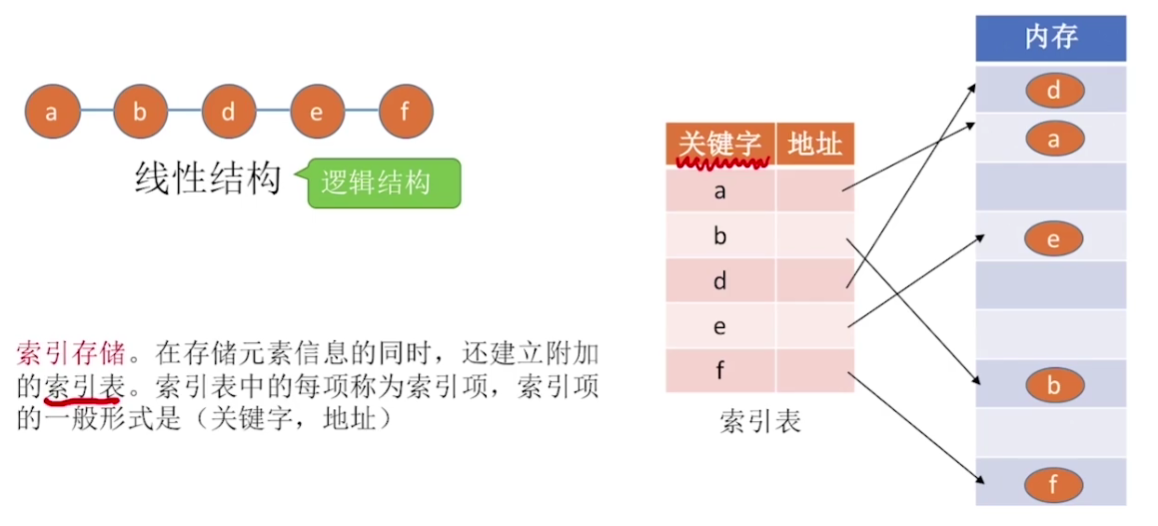
索引存储

散列存储

数据结构的三要素

• 逻辑结构
• 物理结构(存储结构)
• 数据的运算

在声明定义阶段需要声明数据的逻辑结构和对其的运算方法(创建销毁和curd)。而在初始化时则可根据实际情况选择一种存储结构进行初始化，只有这三个条件都满足。才算实现了数据结构

栈（Stack）

栈是只允许在一端[表尾]进行插入或删除操作的特殊线性表

操作分为入栈和出栈，对应线性表的插入和删除

空栈：栈中没有任何数据

共享栈指两个栈共享同一片空间，只出现在顺序表实现的栈中，两个栈一个从栈顶往下写，另一个从栈底往上写

如果使用链表进行初始化栈，它是用头插法在头节点之后进行插入数据和删除数据的，因为链表从头节点向后指，如果想符合后进先出的原则就必须使用头插法，尾插法在每次插入和删除新数据时都需要循环一遍节点，严重影响了性能，头插法的时间复杂度就是O(1)

不带头链表也如此，在最前头进行插入即可。头即为栈顶

队列（Queue）

队列是只允许在一端进行插入，在另一端删除的特殊线性表

操作分为入队和出队，对应线性表的增加和删除

它符合先进先出原则，只能在队头进行出队，在队尾进行入队

使用顺序表实现队列

front存储的是队头元素的下标。而rear存储的是队尾可以插入元素的下标，即当前队尾元素的下一个元素。初始化时就让rear和front都指向0

**队尾指针指向下一个可以插入数据的节点，**因此当数组9下标插完后应指向10，通过取余重新指向了0，如果此时0是有数据的则会符合对头等于队尾的判断，表示为空队列，为了避免判断重合则可以牺牲一个存储单元，在当他为9时则进行判断是否已满，如果不相等则说明0下标的元素已经被取走，可以继续存储，从而形成了一个环状的逻辑。判断是在存储之前进行，因此判断0下标是否相等时是往9下标插入数据[放弃了一个存储单元]。

因为顺序表静态数组是固定一个大小的，因此就需要通过循环队列取模的方式来将有限变为无线，逻辑上扩大了存储范围

计算元素个数则可以用 (rear+MaxSize-front) %MaxSize 用队尾加数组总量再减去队头指针 最后取余。要注意的是rear指的是队尾指针的下一个可插入的元素，而不是当前元素

存满就是MaxSize-1 ，因为舍弃了一个数据单元

使用单链表实现队列则是定义队尾和队头的指针即可，初始化时头尾都指向头节点，如果是不带头节点的话则头尾都指向null

中缀表达式、前缀表达式、后缀表达式

因为计算机是顺序读取，因此在日常中常见的中缀表达式对于计算机来说是无法处理的（要判断括号），将其转换成前缀或后缀表达式才可以理解（直接从头到尾挨个计算就可以了）。因此编译程序就会将中缀转成计算机可以理解的表达式，然后通过机器指令传给计算机计算

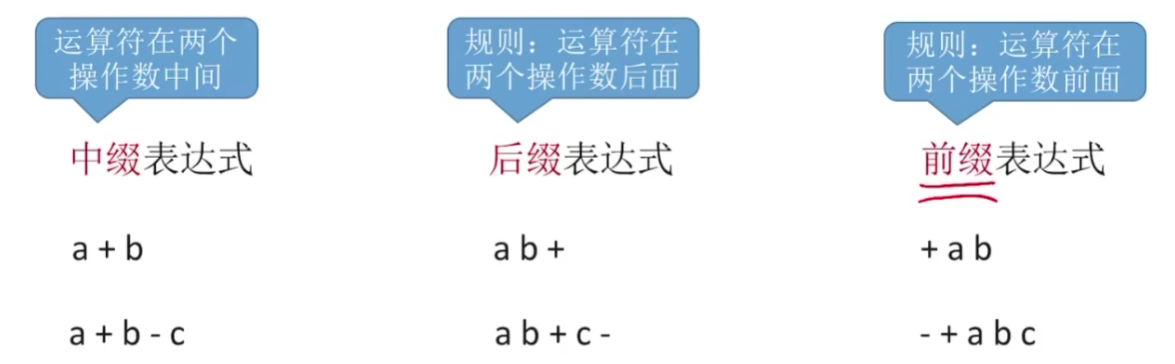
后缀表达式可以根据左优先原则，只要左边的运算符能先计算，就优先算左边的

要注意的是： 先出栈的是“右操作数”，若表达式合法，则最后栈中只会留下一个元素，即最终结果

KMP算法

next[2]时，S只能为1，因此无论串的长度内容多复杂，它的S的最长相等前后缀长度都是为0，因此next[2]永远确定是为1的

next[1]=0时，会让主串和模式串的i,j都往后移动一位，重新开始匹配，因为第一位都对不上了，就只能都后移重新匹配

如果不会经常出现字串和模式串部分匹配问题，使用KMP算法的意义并不大。

树

树是从上往下的，因此树的结点路径只能从上往下计算，路径长度则是经过了几条边

结点的度指的是有几个子节点。树的度则是指每个节点的度的最大值，最大值则等于树的度

树分有序树和无序树，如果同一层结点的左右位置反映某些逻辑关系则是有序树，反之是无序树

子节点及子节点向后的节点也可以合并称之为子树，如A节点有三棵子树。B及下面所有，C及下面所有等

完全二叉树如果某个节点只有一个度，那么它的子节点一定是左子节点

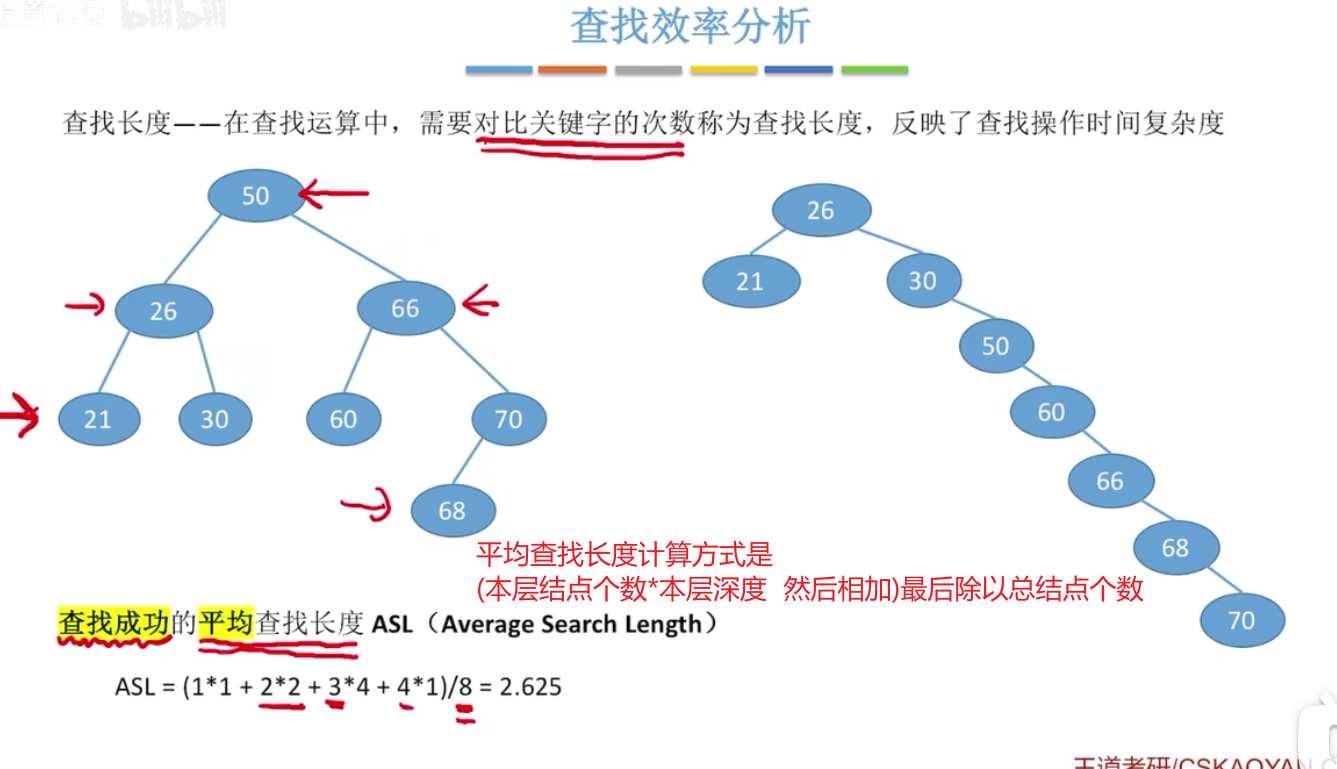
因此设计平衡排序二叉树尽量的宽，高度尽量低

二叉树

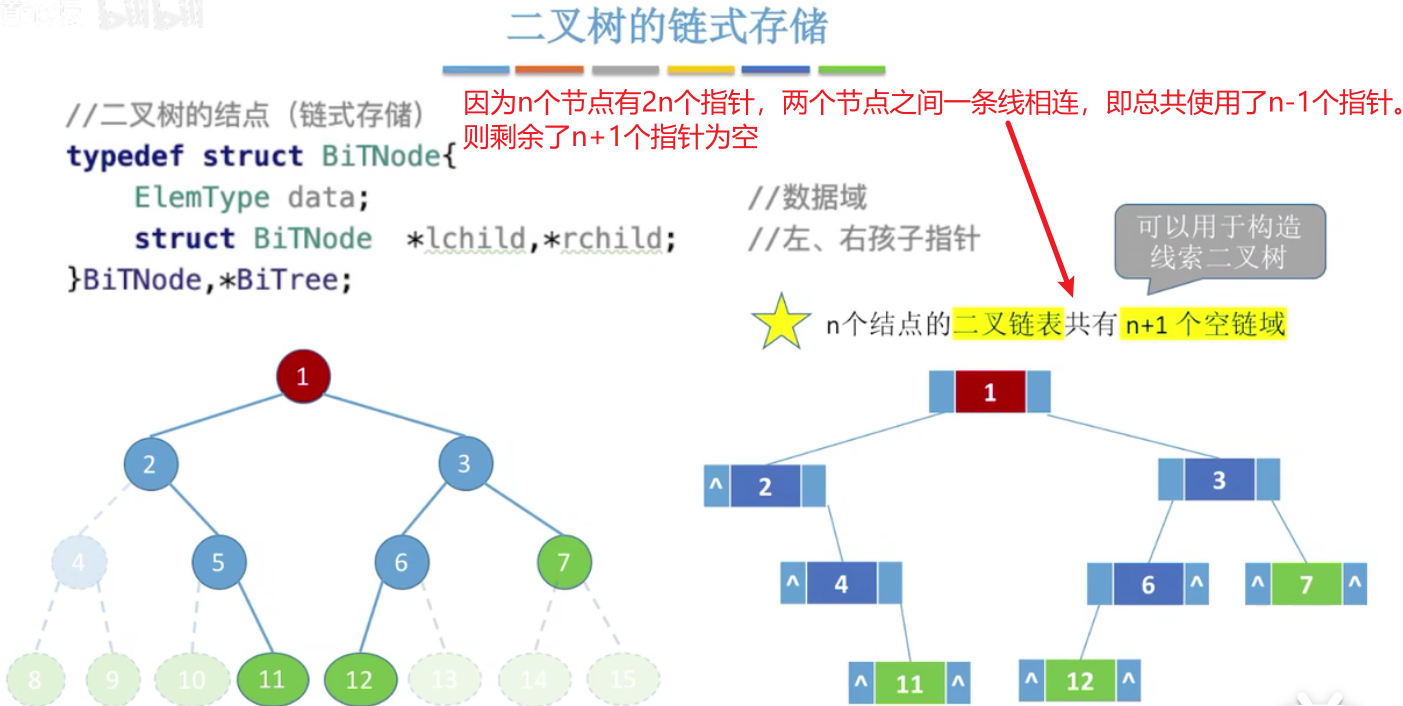
n个节点只需要n-1个指针就能连接，剩余了n+1个空指针

如果经常要查询对应节点的父节点就需要使用三叉链表，多存储一个指针来存父节点的指针

二叉树的先中后序遍历

采用分支节点逐层展开发

二叉树的层序遍历

如果要通过序列推算出二叉树的形状，一定是 前/后/层级+中级两个才能共同确定出一个树的形状。胡乱搭配是无法推算出的

线索二叉树

二叉树找前驱和找后继必须要重新遍历一次才行，因此将**空闲的左孩子指针和右孩子指针[空链域]**充当为前驱和后继，并设置一个tag标志就可以实现线索二叉树

树的存储结构

森林和二叉树的转换

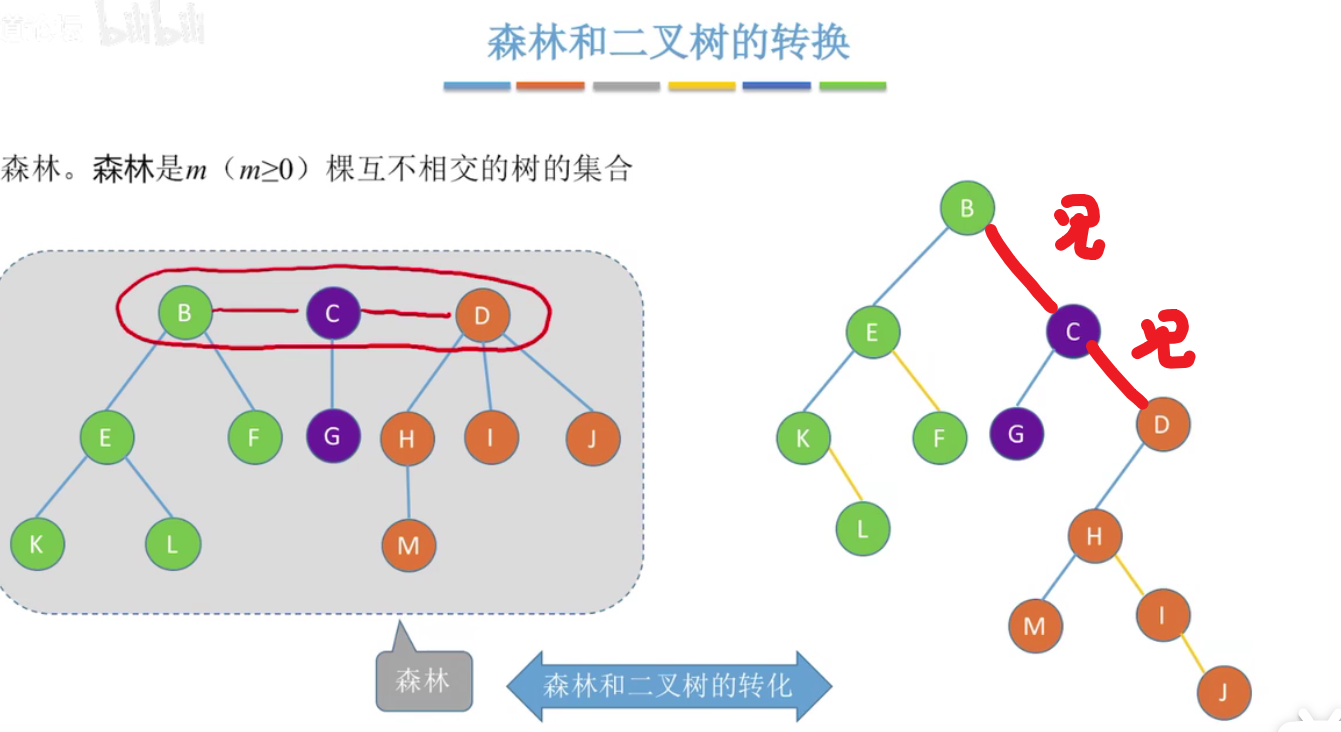
二叉排序树

二叉排序树的查找效率很大程度上取决于树的高度

平衡二叉树

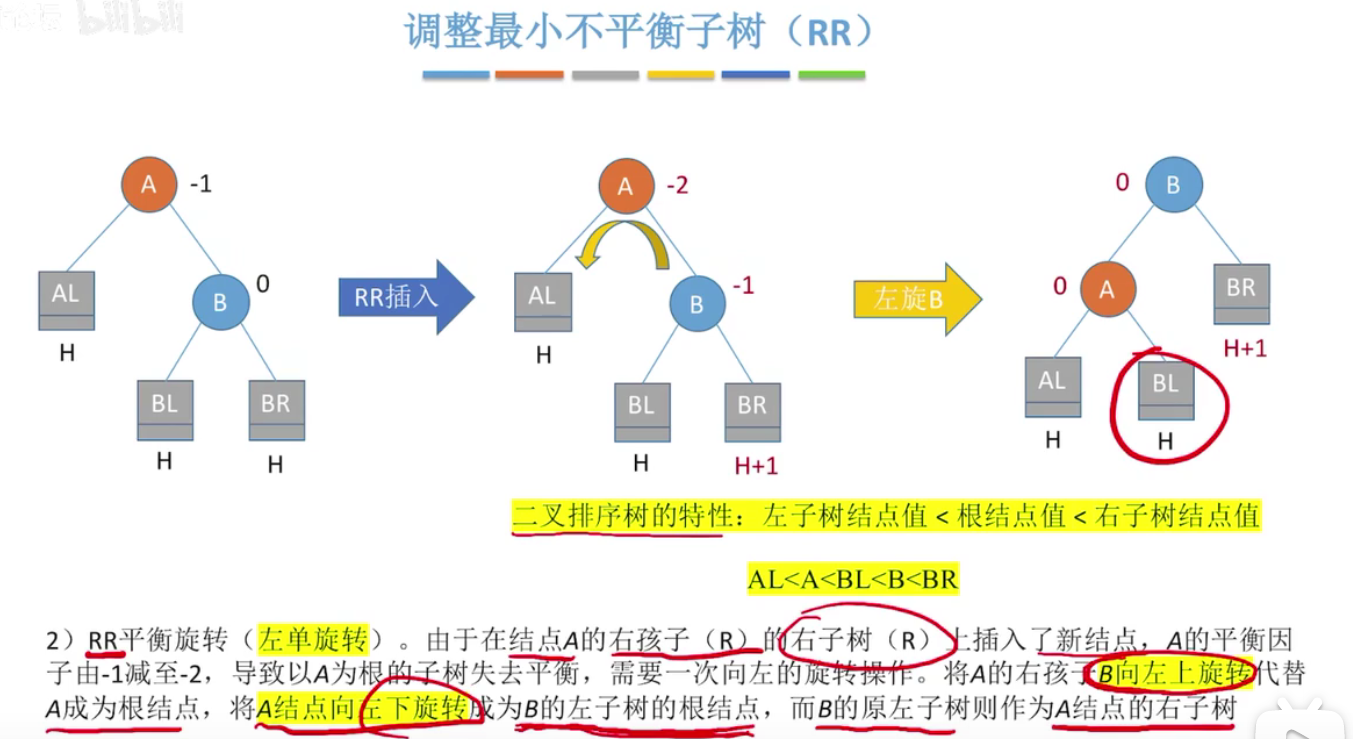
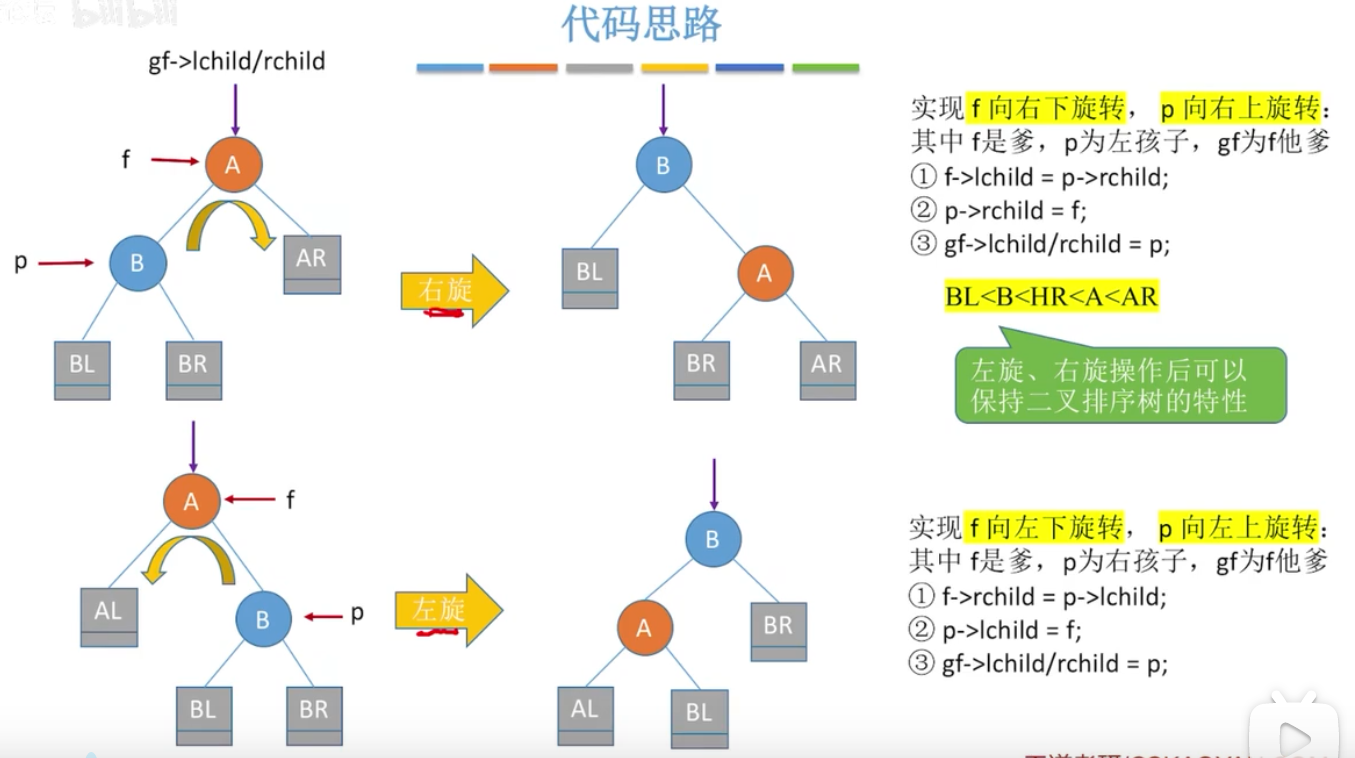
LL和RR

总共有四种情况，记住左孩子只能右上旋，右孩子左上旋即可。

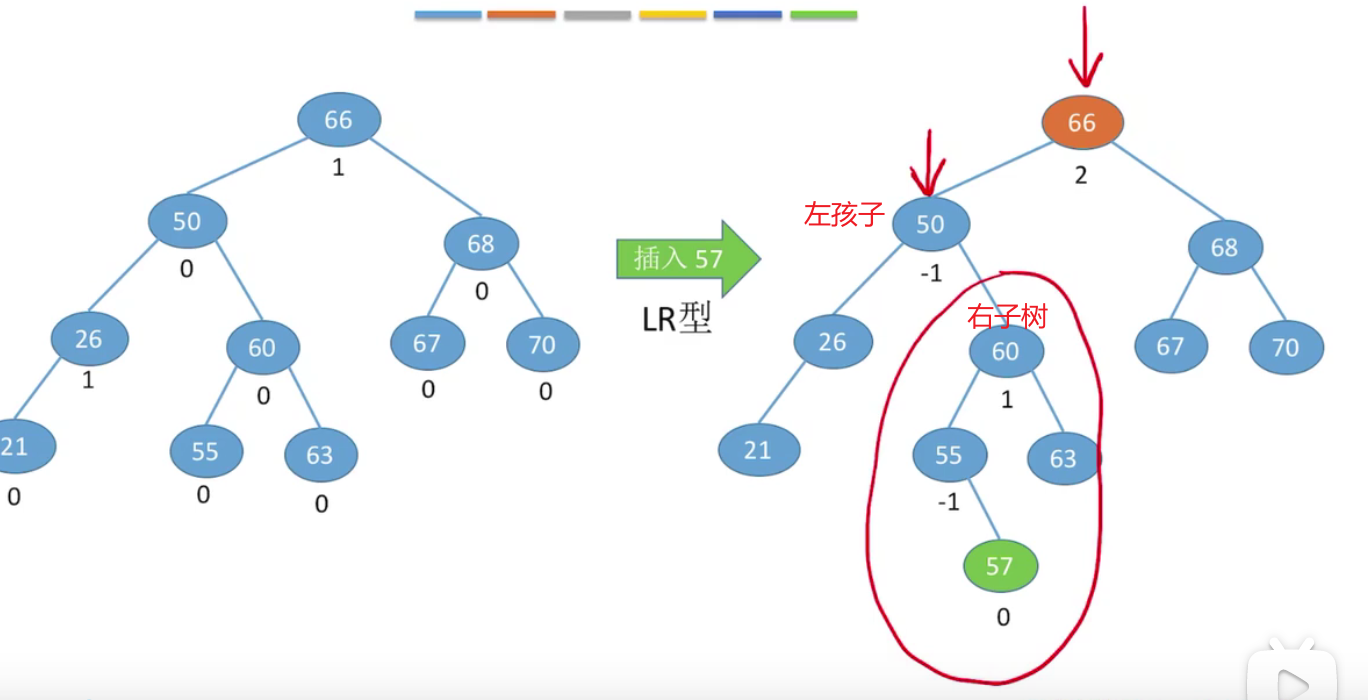
一定要注意的是，在A结点的B孩子的子树上插入节点，并不意味着子树原先就是叶子节点，它可能是分支

在第一次出现大于1的地方，这个节点和它下面的节点组成最小不平衡子树。

哈夫曼编码

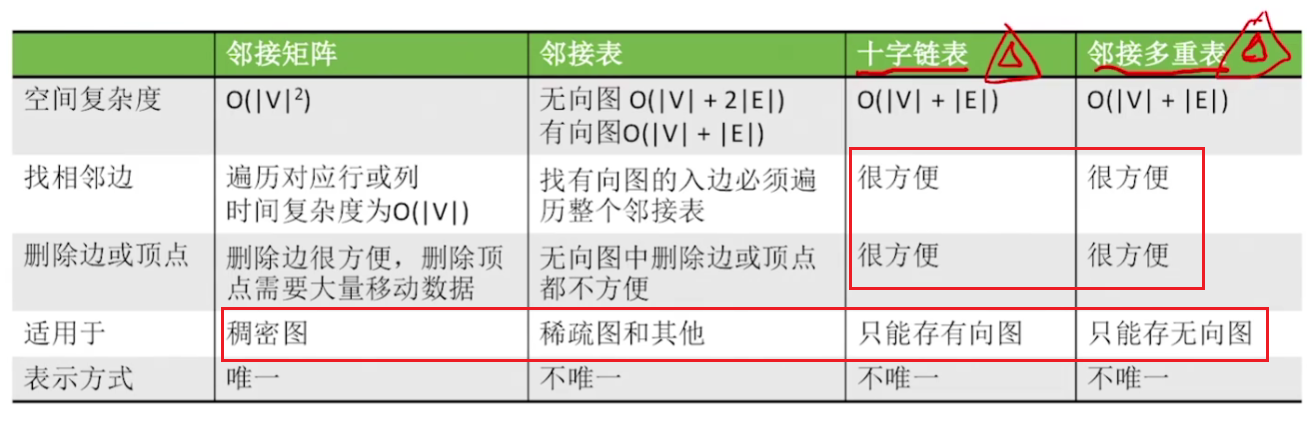
图

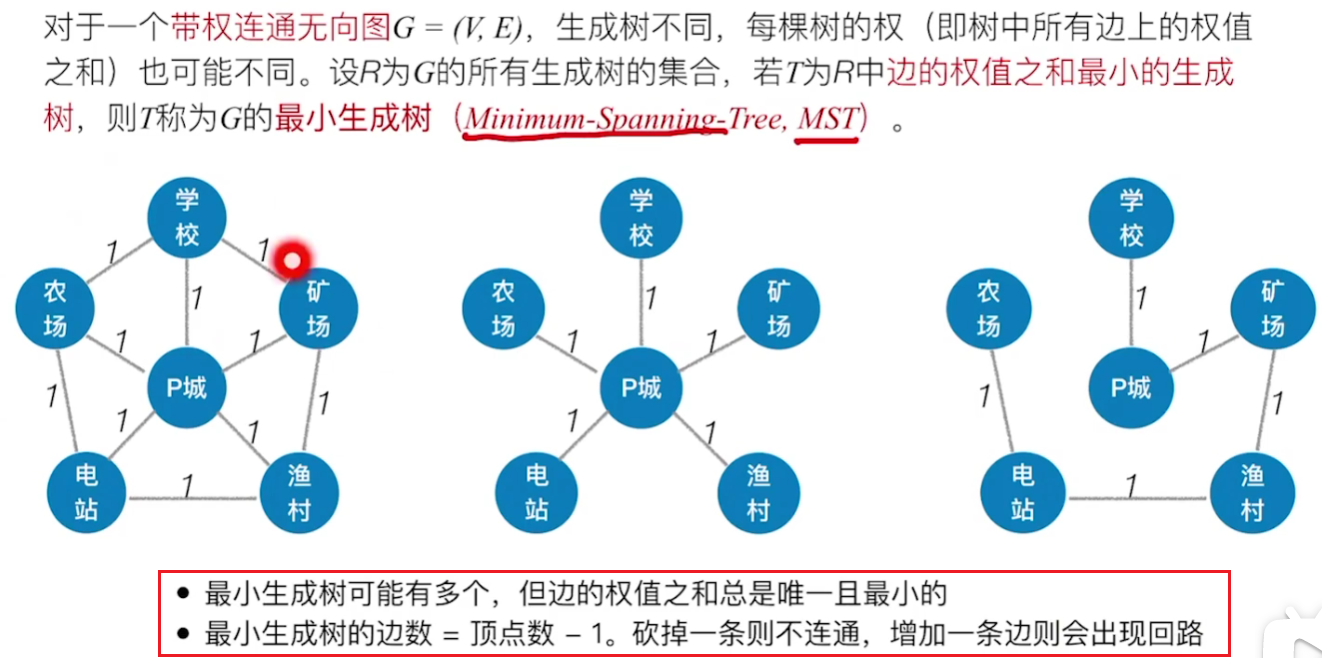
最小生成树

在P城和矿场连通后，此时从渔村到P城已经有路线了，因此P到渔村的直线边即使权值最小也不能进行连接

排序

快速排序

快速排序算法是所有内部排序算法中平均性能最优的排序算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

func main() {
	translate := [10]int{4, 78, 37, 49, 22, 77, 31, 57, 27, 19}
	QuickSort(&translate, 0, 9)
	fmt.Println("arr:=", translate)
}

// 用第一个元素作为基准划分为左右两部分,low左指针，high右指针
// 这个方法可以让基准左边的都小于基准，右边的都大于基准，但是不能保证左边和右边是有序的，它们仅仅是都大于或小于基准
// 紧接着通过阶乘的方式缩短范围，直至缩短到low和high不满足条件位置(low>=high)
func partition(translate *[10]int, low int, high int) int {
	pivot := translate[low]
	// if low >= high 跳出循环
	for low < high {
		// 比较右指针的数据是否比pivot大，大则继续往前移动
		for low < high && translate[high] >= pivot {
			high = high - 1
		}
		// 原先的基准被pivot暂存，因此可以覆盖
		translate[low] = translate[high]

		// 比较左指针的数据是否比pivot小，小则继续往前移动
		for low < high && translate[low] <= pivot {
			low = low + 1
		}
		// high的数据放在了原基准的位置，可以覆盖
		translate[high] = translate[low]
	}
	translate[low] = pivot
	// 返回存放基准的最终位置
	return low
}

// 快速排序
func QuickSort(translate *[10]int, low int, high int) {
	if low < high {
		// 划分
		pivotpos := partition(translate, low, high)
		QuickSort(translate, low, pivotpos-1)
		QuickSort(translate, pivotpos+1, high)
	}
}

各种排序方法的综合比较

时间性能

空间性能

操作系统小结

进程相关的原语有 创建原语、撤销原语、阻塞原语、唤醒原语、切换原语

短作业优先

优先级调度算法

多级反馈队列调度算法

PV

因此最好只在临界区里面做最重要的操作

互斥是指对某一临界资源在某段时刻只能有一个进程使用，PV写在同一进程中，初始值为临界资源的数量。

同步则是一个进程的发生需要等待另一个进程结束或到某一结点，通常根据实际情况设置初始值，需要在先发生的进程中进行V操作，后发生的进程中进行P操作，这样如果处理机先执行后一个进程也会因为P的值小于0导致进程从运行态转变为阻塞态，直到对应V操作+1以后重新从等待队列唤醒对应进程进入就绪态

苹果问题（多生产者多消费者）

当缓冲区为1时，由于同一时刻至多只有一个大于0，其他都为0，就可以省略mutex互斥

吸烟者问题（一生产者多消费者生产不同类型的消息）

读者问题（写者互斥，读者可同时读取）

哲学家问题（进程需要同时持有多个临界资源且每个进程互斥）

管程

管程中有很多个入口（函数），但是每次只会开放其中的一个入口给某一个进程使用。如在生产者消费者问题中，各进程需要互斥的访问共享缓冲区。管程的这种特性即可保证一个时间段内最多只有一个进程在访问缓冲区。要注意的是：这种互斥特性已经由编译器帮忙实现了，程序员并不需要关心，程序员只需要调用特定的管程方法操作管程即可，其中的细节已经封装到底层了。

死锁

银行家算法

在每次分配资源时先判断这次分配资源是否会发生不安全状态，造成死锁

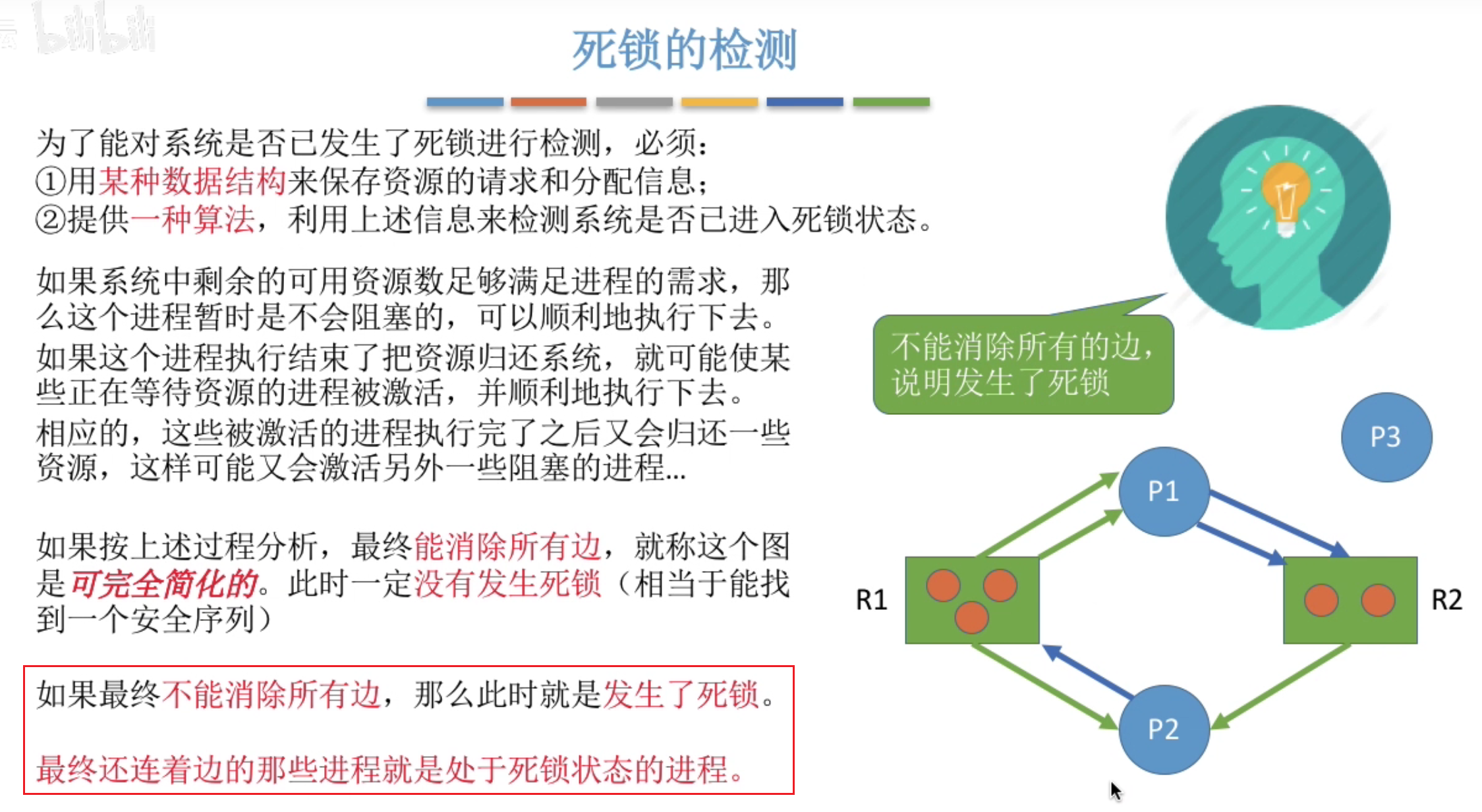
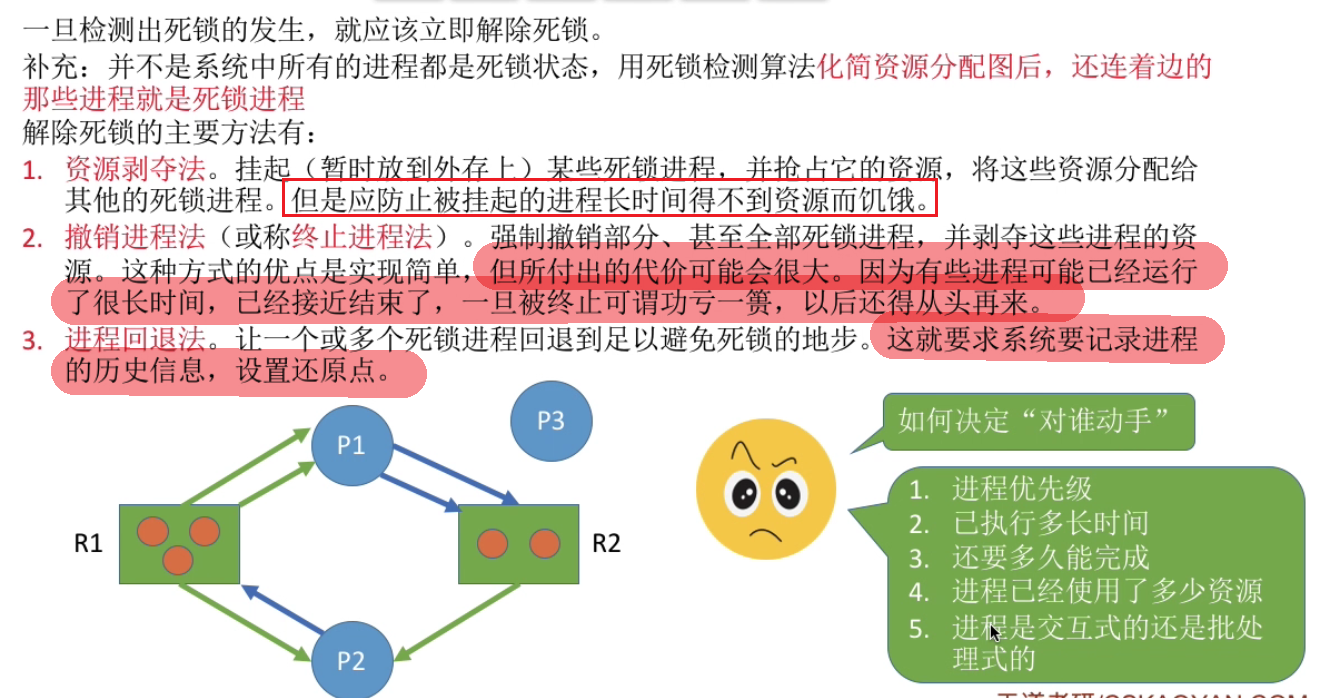
死锁的检测

死锁的解除

内存知识

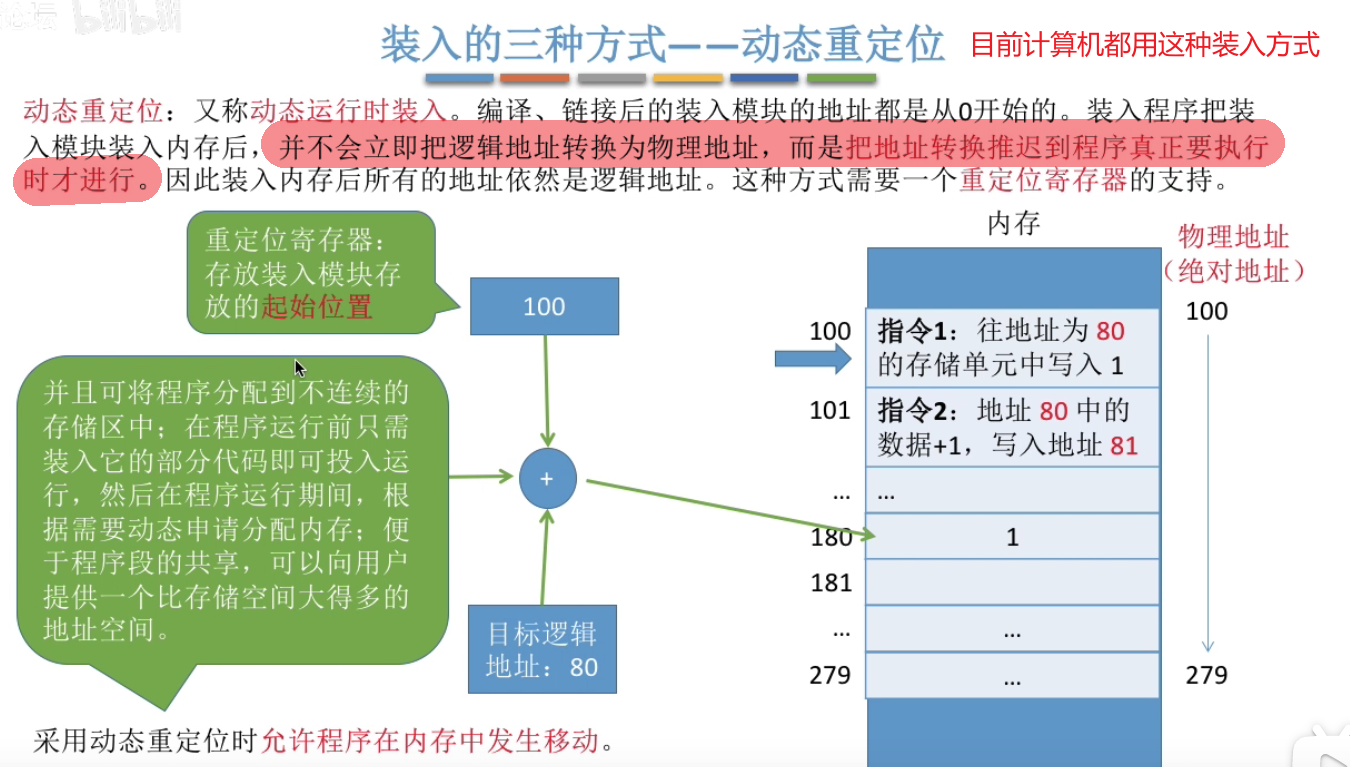
动态重定位：在程序装入内存中时，程序段中的依然还是逻辑地址，只有当程序运行时，cpu会读取重定位寄存器存放的起始位置(程序运行时会先将起始地址从pcb存到重定位寄存器中)，将它与程序段中的逻辑地址相加计算就可以得到物理地址。这是当代计算机使用的装入方式最优解

基本分页存储管理

cpu在得到逻辑地址后，需要访问两次内存，第一次访问是查页表，第二次则是访问目标单元

系统仅有一个页表寄存器，而在PCB记录的是这个进程对应的页表。一个系统中可能会有多个页表对应多个进程。当程序运行时就会将PCB的页表数据覆盖给页表寄存器中

快表

基本分段存储管理方式

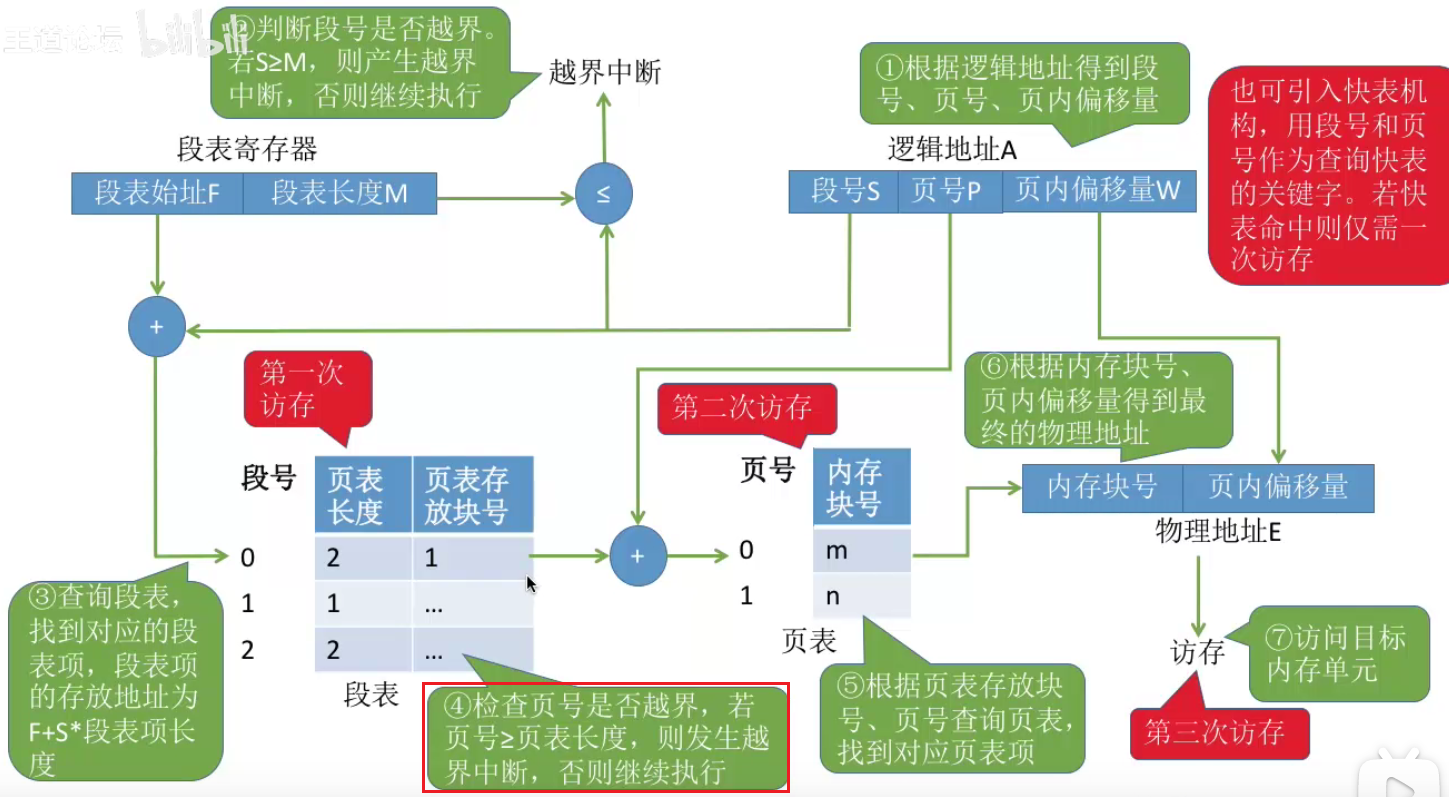
段页式管理方式（分页和分段经典折中）

一个进程有一个段表，但是可能会有多个页表（因为每个段表都对应一个页表）。而使用段页存储时，内存是划分为固定长度的多个小区间，因为段页存储最后是由页去操作实际地址

用户只需要提供段号和段内地址，因为分段是用户可见的，而分页是由操作系统进行分页的，是对用户不可见的，操作系统会帮用户将段内地址拆分为页号和页内偏移量。因此这个存储管理方式是二维的。

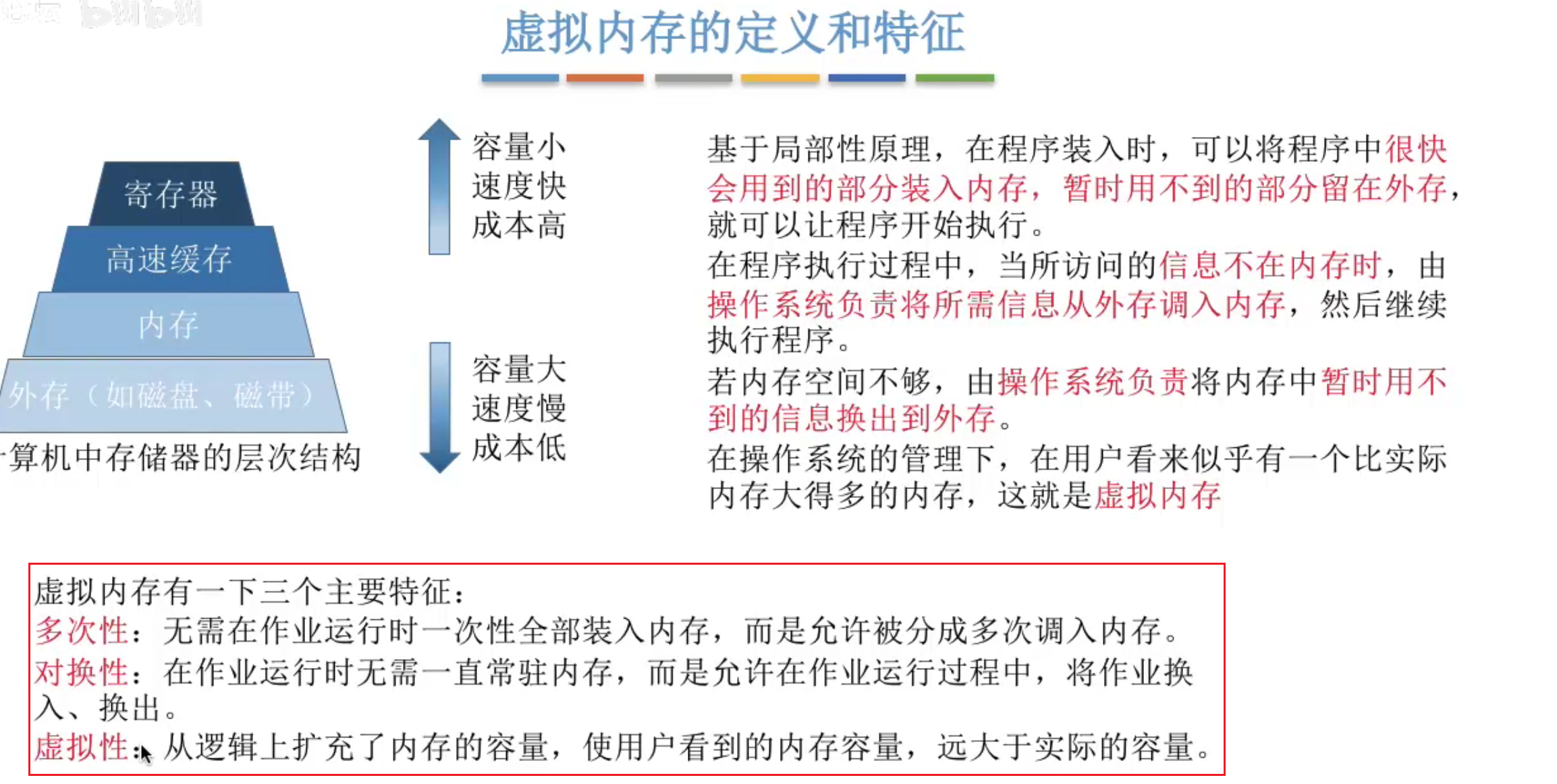
虚拟内存（目前计算机主流设计方案）

前面几个内存存储管理方式有很多缺点，最大的缺点则是只能一次性将数据全部存入内存中，这会导致过大的程序无法运行在小内存中

请求分页管理方式

要注意的是：只有写指令才需要修改 修改位，并且，一般只修改外存中的修改位即可。这样可以减少访存次数。但是如果是将某个页面换回外存，则需要先将外存最新的数据写回慢表中，然后删除快表对应数据，然后慢表将数据覆盖到外存忠，最后修改对应慢表数据。

在页面调入内存后，不仅需要修改慢表的数据，页需要将表项复制到快表中。这样查询就可以减少访存次数。

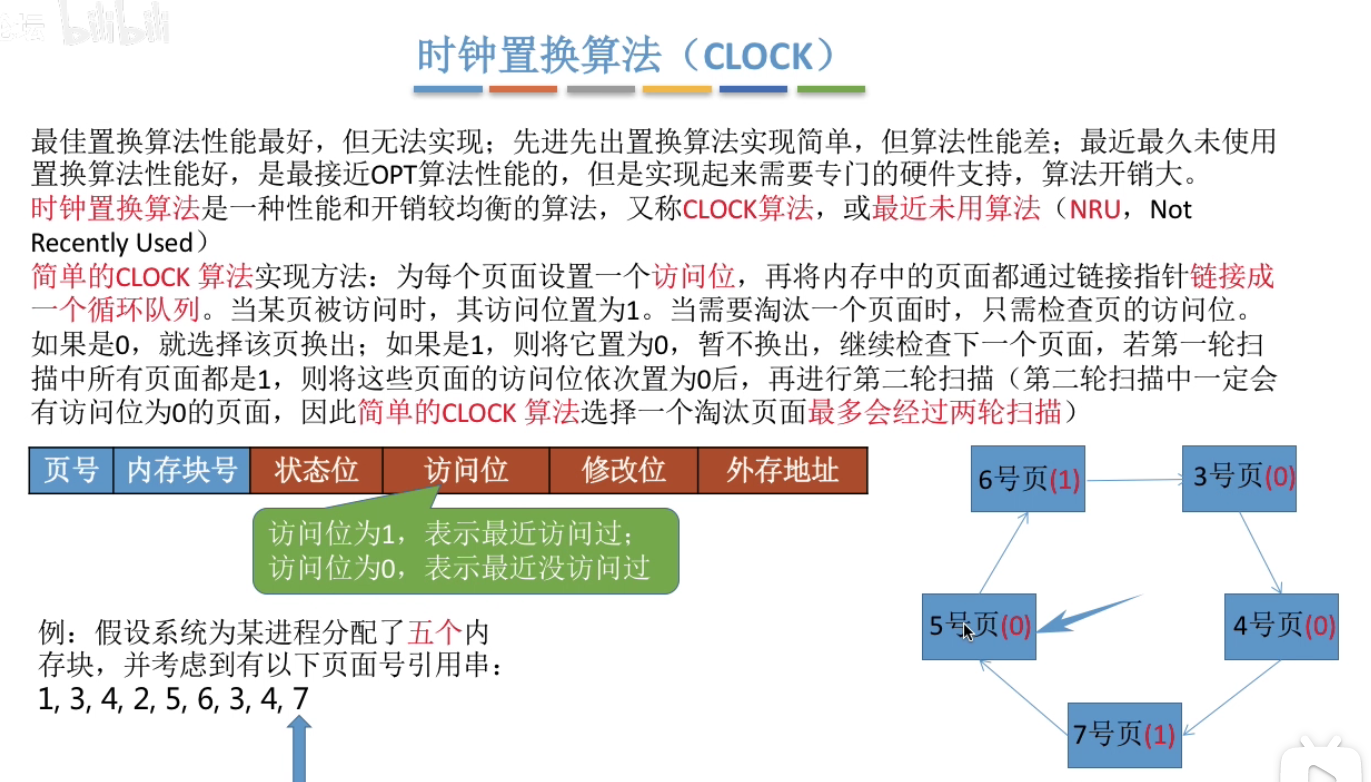
页面置换算法

通过四轮扫描就可以发现，第一轮先淘汰最近没访问且没被修改过的页面；第二轮淘汰最近没访问但被修改过的页面；第三轮经过第二轮将其访问位都改为0后，淘汰的就是最近访问过但是没有修改过的页面。第四轮则是淘汰最近访问过并且修改过的页面。

驻留集是指系统给进程所分配的内存块的集合

文件管理

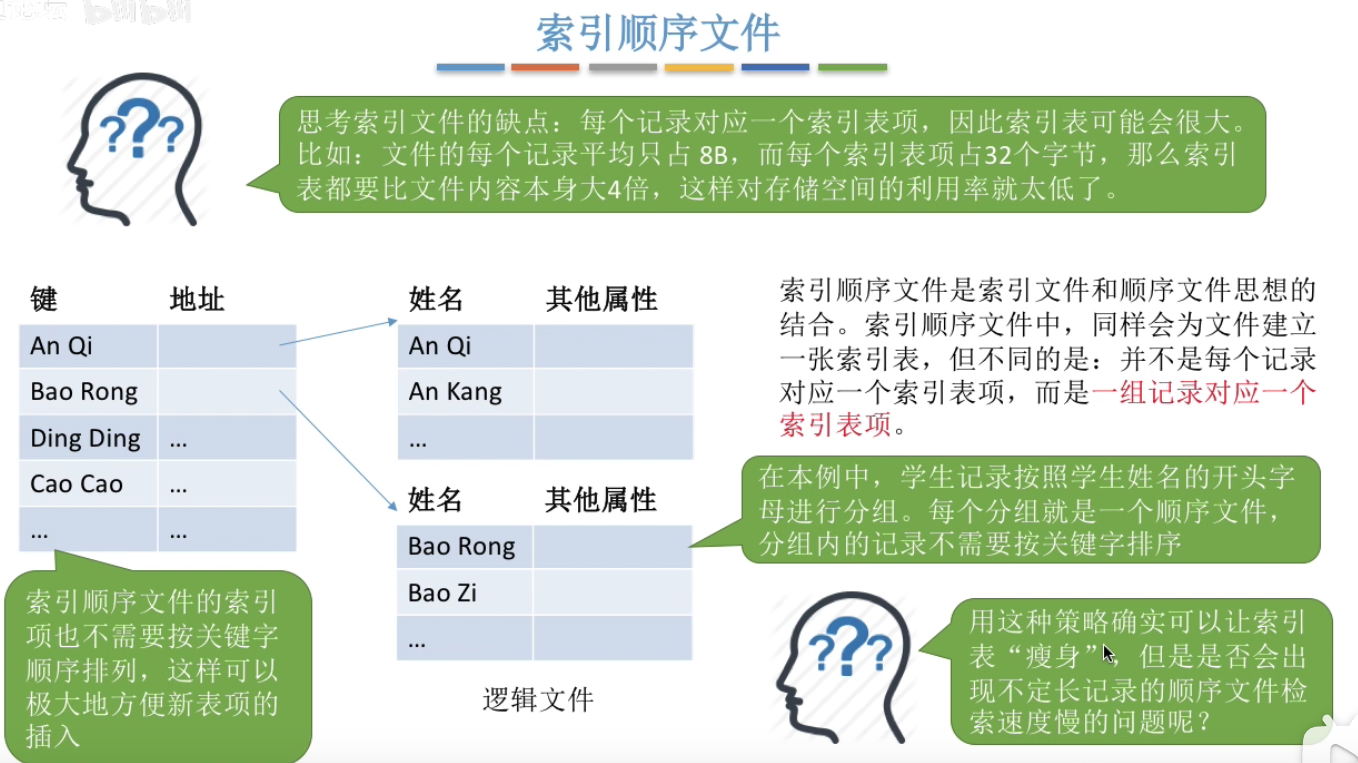
索引顺序文件

目录结构

文件分配方式-索引分配

但是如果每个索引块中只有一个表项有实际指向数据，就会造成极大的浪费以及不必要的多次读盘操作，

因此混合索引诞生解决了此问题。

磁盘调度算法

I/O相关知识

DMA

采用DMA之后数据就不再需要先存到cpu寄存器中再转存内存了

DMA控制器读写数据的基本单位依然是一个字，但是以读来说，它会先从磁盘中读入一个字放入DR，然后DR再放到内存。然后进行下一个循环，直到读完一个块的数据后(读完DC需要的字节数)，才会给CPU发出中断。

通道控制方式

通道程序就是一系列针对I/O的通道指令，这种方法CPU干预率进一步降低，通道只有在读取完CPU指定的全部数据后才会发出中断